AlexNet
AlexNet是第一个真正意义上的深度卷积神经网络,其在2012年由Alex Krizhevsky、Ilya Sutskever和Geoff Hinton提出:https://proceedings.neurips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf,借鉴LeNet结构,将深度做到了更深,在2012年ImageNet图像分类大赛中大放异彩。
AlexNet的成功主要有两点关键因素,首先是ImageNet数据集在2009年被提出并公开举办ImageNet图像分类挑战赛,LeNet用于的手写数字识别数据集是一个很小的数据集,支撑不起来深度神经网络,而ImageNet数据集则有100万个训练样本,1000类数据,这给深度学习领域发展作出了极大的贡献。第二点则是算力的进步,卷积神经网络中存在的矩阵运算更适合在GPU上进行,因为CPU一般核心数较少,即使核心频率高也比不过动辄上千个核的GPU,AlexNet则是可以在硬件GPU上进行加速的网络,其使用两块GTX 580 GPU实现了快速卷积运算,从而使得深度网络成功有了可能性。
Alex结构如下(图来自李沐老师的《动手学深度学习》):
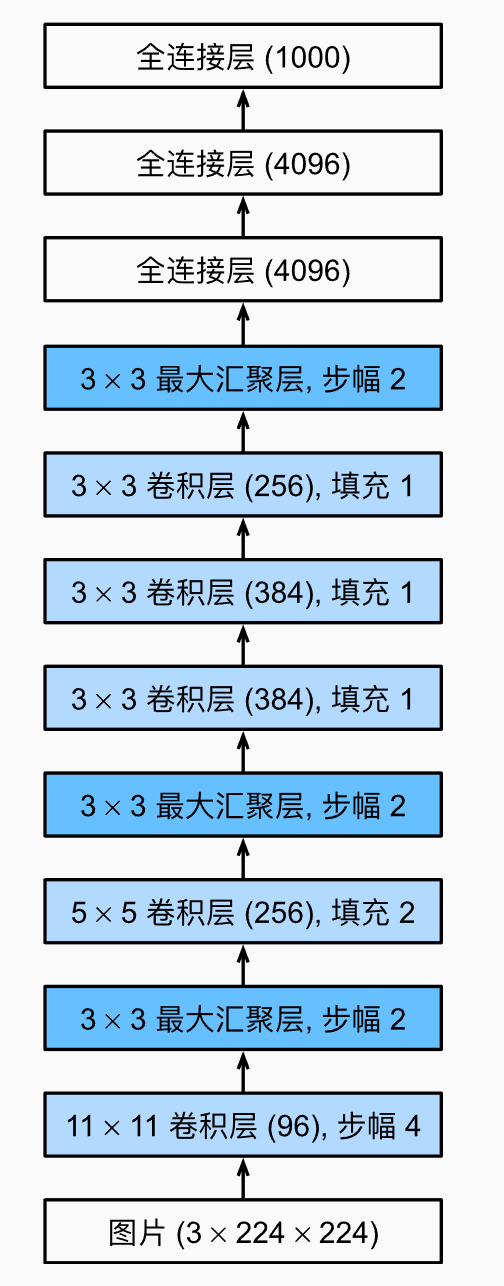
可以看到它和LeNet非常类似,都是在若干个卷积层后面加入汇聚层(池化层)作为特征提取器,最后使用全连接网络来对提取出的特征进行分类。由于ImageNet图像大小比较大,且最终分类数为1000,因此网络卷积核大小以及最后的输出都需要调整。
这个结构实现起来也比较容易,使用pytorch实现如下,这里将最终的分类数变成了10,并且输入图片为黑白图片(单通道图片,一般处理图片使用RGB 3通道图片),这样便于使用小的数据集进行验证:
1 | class AlexNet(nn.Module): |
VGG
AlexNet的成功证明了深度卷积神经网络的有效性,VGG网络则是设计更加规整的深度卷积神经网络,其将网络设计成由很多个块进行拼接,这简化了网络设计,VGG是在2014年ImageNet竞赛中提出:https://arxiv.org/pdf/1409.1556.pdf。
VGG网络由若干个VGG块加上后面的全连接网络组成,每个VGG块包含若干卷积层、Relu层以及汇聚(池化)层。前面卷积部分用于特征抽取,后面全连接部分用于分类。
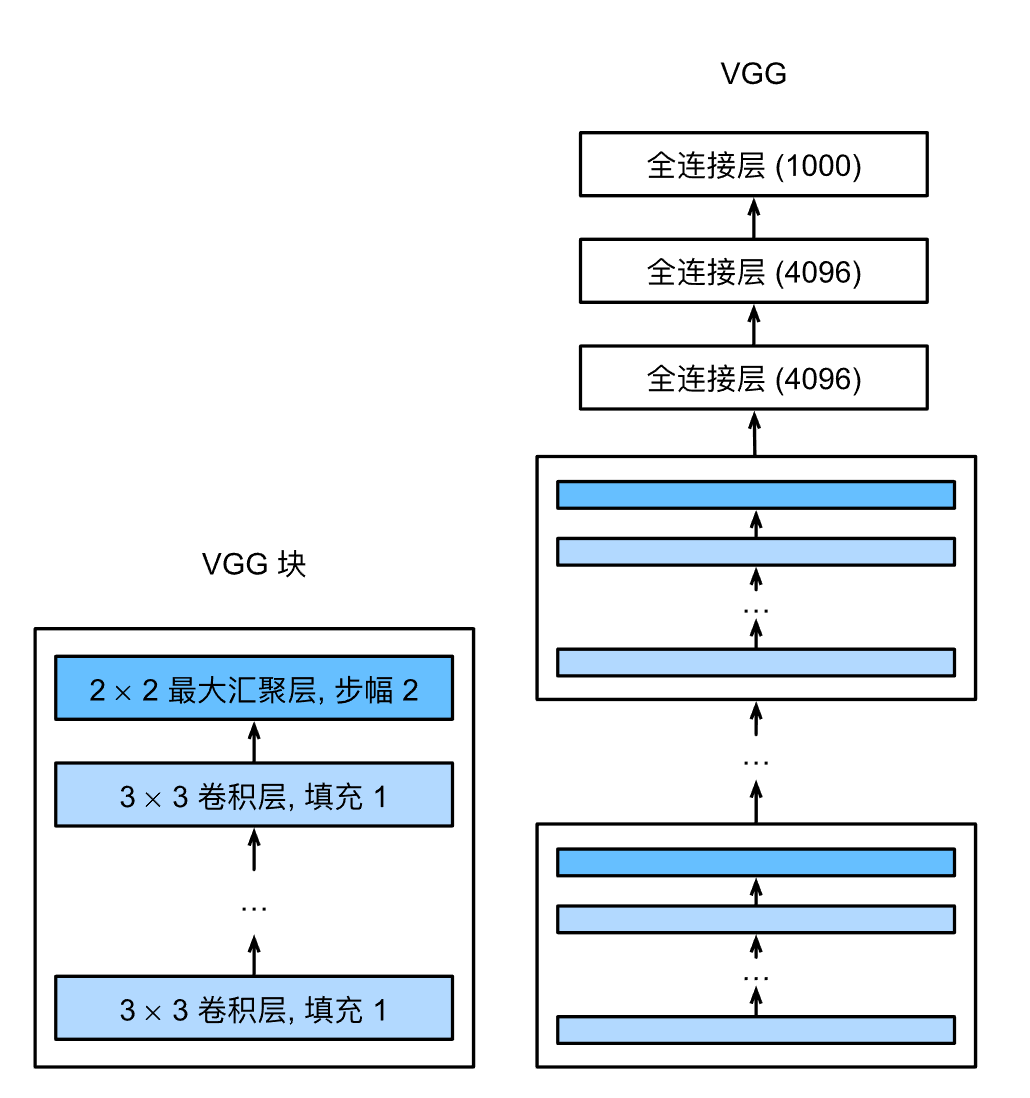
实现则是先实现vgg_block,每个vgg_block可以有不同的卷积数量,卷积都采用3x3卷积并加以一个像素的填充,这样卷积不改变特征图的大小,只通过最后的2x2汇聚层来将特征图缩小一倍。
1 | class VGGBlock(nn.Module): |
GoogleLeNet
同样在2014年ImageNet图像分类挑战赛中,ImageNet网络架构大放异彩:https://www.cv-foundation.org/openaccess/content_cvpr_2015/papers/Szegedy_Going_Deeper_With_2015_CVPR_paper.pdf,GoogleNet也是使用多个块堆叠而成,这个块被称为为Inception结构,其将不同大小卷积核分成不同通路分别对输入进行计算,最后将结果在通道维度上进行合并,Inception结构如下图所示:
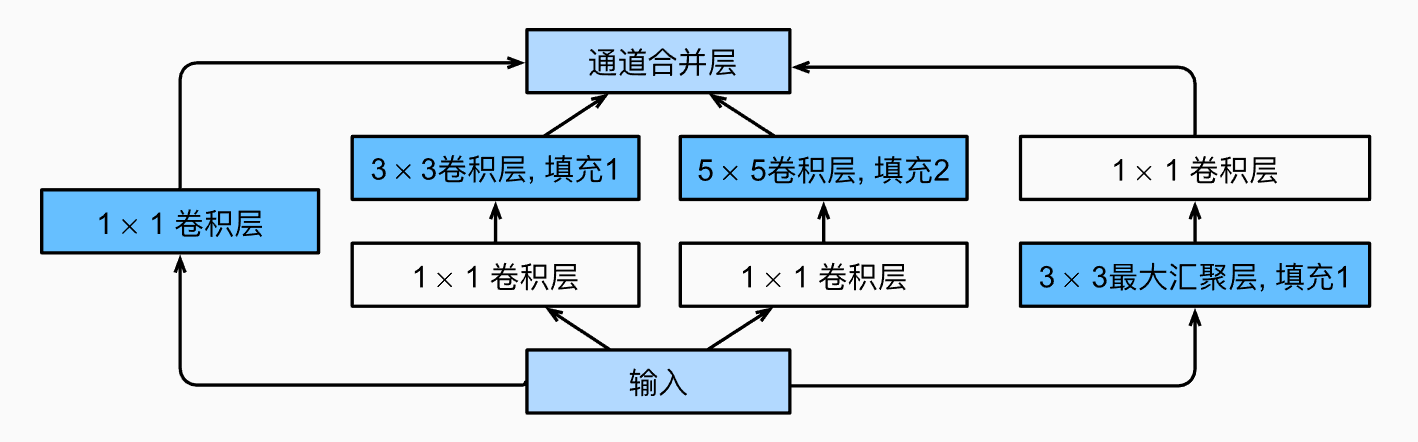
可以看到,该结构对输入特征图经过4条不同的通路进行计算,其中第一条通路只用 1x1 卷积核进行卷积,第二条通路分别使用 1x1 和 3x3 卷积核进行卷积,第三条通路使用 1x1 和 5x5 卷积核进行卷积,第四条通路则是先进行最大汇聚然后再 1x1 卷积。通过不同通道的不同大小卷积获得不同的空间信息。
Inception 结构实现如下:
1 | class Inception(nn.Module): |
GoogLeNet结构如下图所示,其由9个Inception块组成,期间使用最大汇聚层降低特征图的大小,在最后的全连接之前使用全局平均汇聚层将特征图变为1x1大小,后面在通道维度上使用全连接网络分类,实现如下:
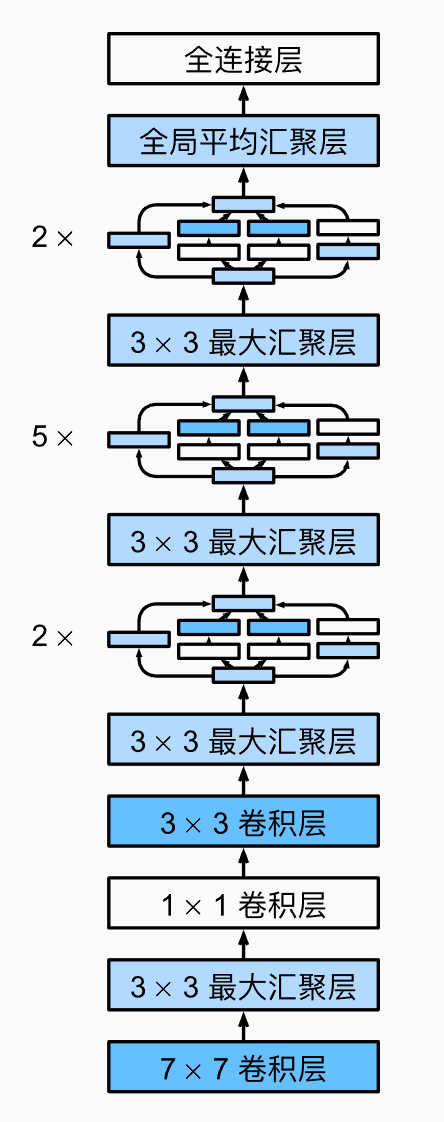
1 | class GoogLeNet(nn.Module): |
ResNet
残差神经网络(ResNet)是2015年ImageNet图像分类挑战赛中何凯明等人提出的:https://arxiv.org/pdf/1512.03385.pdf,主要考虑的问题是如何使网络能够更深、效果更好。
残差块
原论文首先是发现单纯的将原先的网络块进行堆叠时,当到达一定的深度时效果反而会变差,也就是说深度神经网络很难训练且效果不佳。残差块则是为了解决这一问题,作者认为,如果一个新的复杂网络函数\(f'\)能够包含原有的函数\(f\)的话,原理上来说,必定存在一组网络参数使得网络效果不比原来的更差。 残差块的结构如下图:
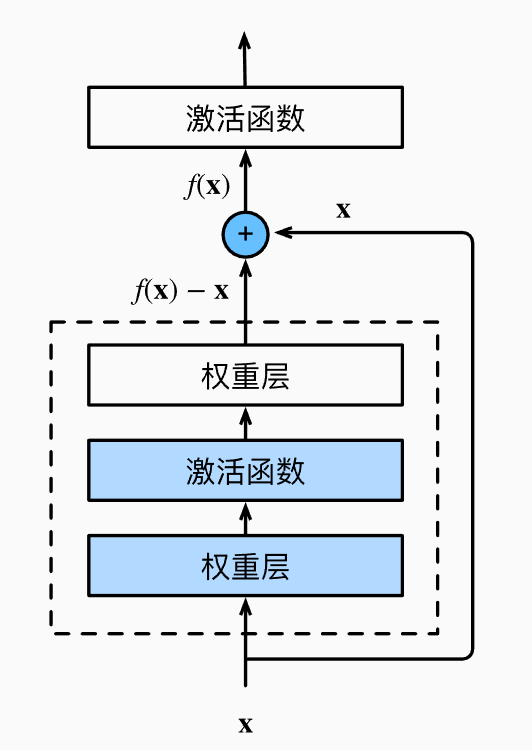
它在正常的通路的基础上添加了一条直通通路(shortcut),注意图中加号是指特征图按像素相加,这样的话从原理上讲残差块至少可以拟合一个恒等映射,也就是权重层参数均为0,这也是ResNet能够将深度做得很深的原因。
实际使用的残差块分为以下两种,一种是直通通路上存在 1x1 卷积操作,这样可以改变残差块的输出通道数;另一种是直接将输入连接到输出处,这种残差块输入通道数和输出通道数必须相等。
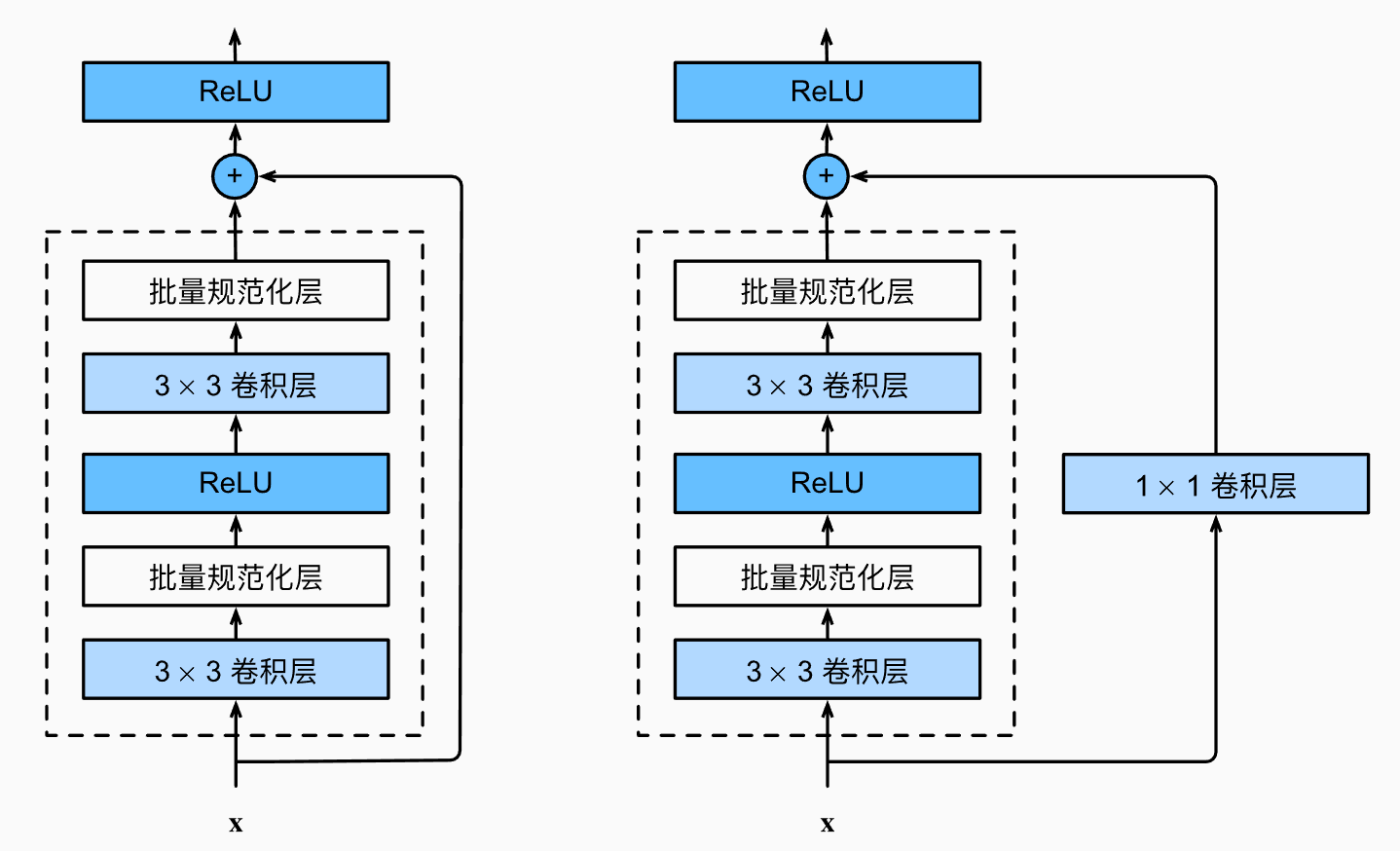
这两种残差块的实现如下,用use_1x1conv参数标识残差块的类型:
1 | class Residual(nn.Module): |
残差神经网络(ResNet)
ResNet就是将多个残差块进行堆叠而成,实际上ResNet论文中提出了多个不同深度的版本,可以根据任务的复杂程度以及实时性需求选取不同的网络:
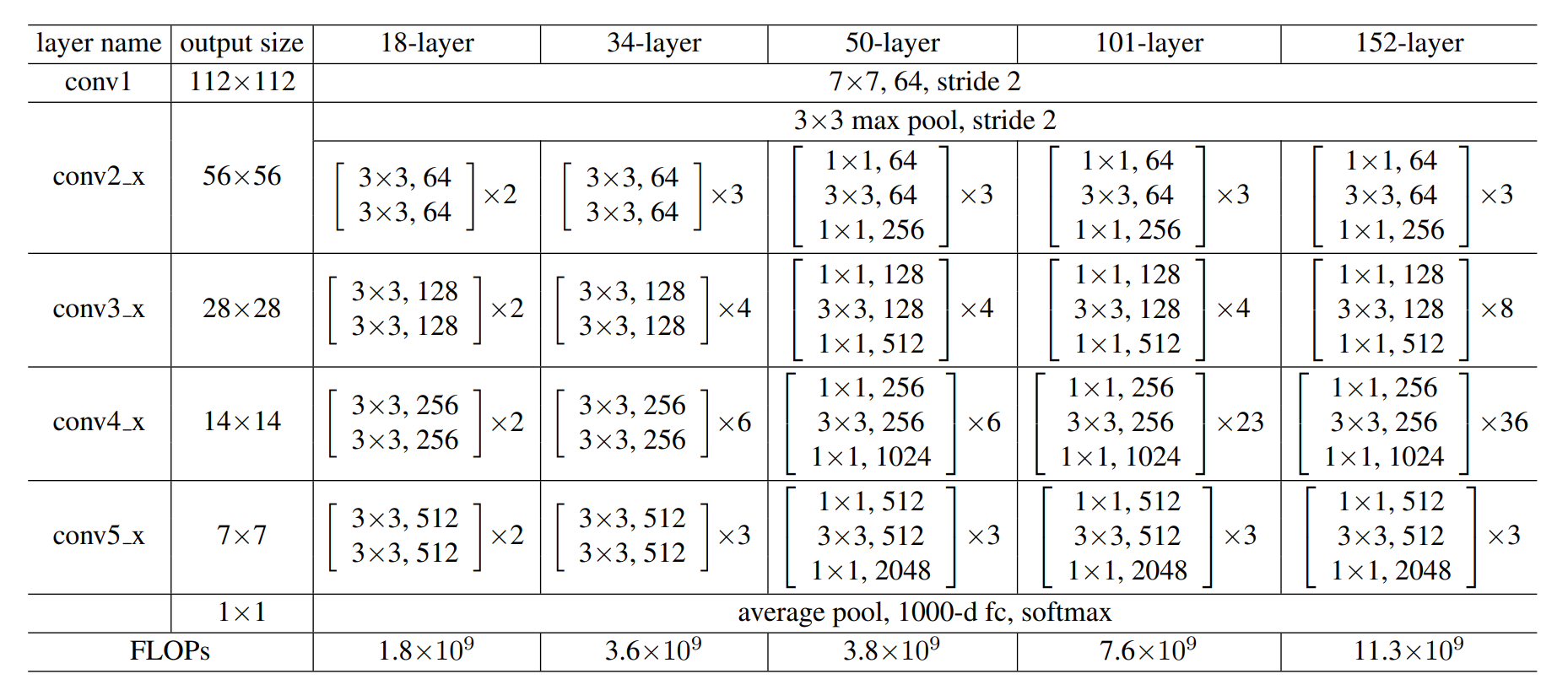
其中 resnet-18 实现如下:
1 | class ResBlock(nn.Module): |
总结
本片博客总结了部分目前典型的卷积神经网络结构,这些网络都是现在常用的图像特征提取器。


