深度学习系列（一）：卷积神经网络

#深度学习 2023-03-07

前言

之前学习了全连接神经网络并将其运用在MNIST手写数字的数据集上，能够取得一定的准确率，但是对于图像的识别，我们有一种更高效、更准确的神经网络模型：卷积神经网络（Convolutional Neural Network）。这种网络相较于全连接神经网络而言，更能够体现出图像像素相对位置的影响，而且需要训练的参数更小，对于全连接神经网络而言，网络层数增多之后训练起来难度很大，且伴随着梯度消失问题，卷积神经网络也一定程度上解决了这种问题。

目前，卷积神经网络已经成为了深度学习领域最为常用的结构之一，很多新的深度学习应用里面都使用卷积层来提取特征。

ReLU激活函数

首先介绍一种激活函数类型：ReLU函数，我们对比一下ReLU和Sigmoid两种激活函数。

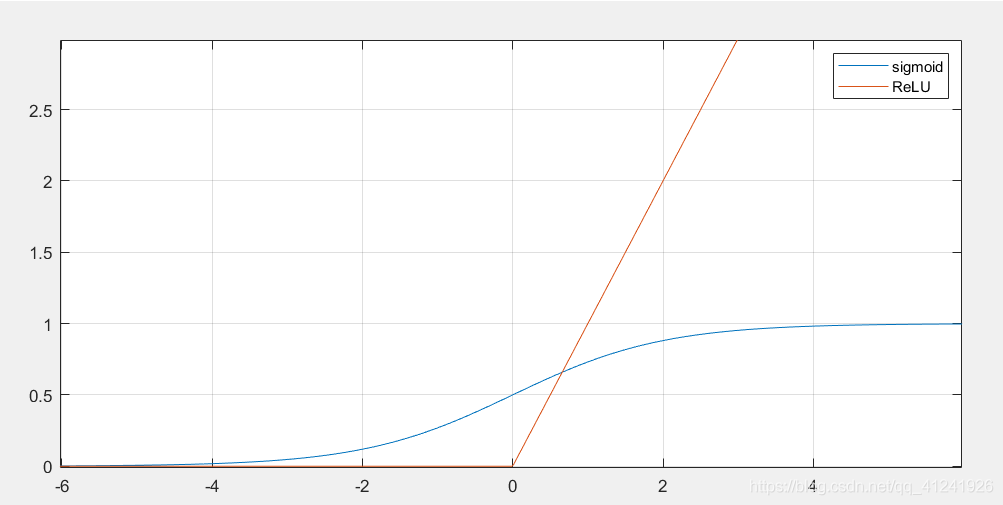ReLU和Sigmoid对比 ReLU函数的表达式为：

\[ f(x) = \begin{cases} x & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases} \]

也可以直接表示为对$0$和$x$求最大值。这个ReLU函数是2012年Alex在AlexNet中使用的，也是现在广泛使用的激活函数。ReLU函数有几个特点：

能够避免BP网络训练过程中的梯度消失问题，从梯度推导可以知道，反向传播时每传播一层就会乘以一个激活函数的导数，对于Sigmoid函数而言，它导数的最大值为$0.25$，神经网络的层数一多就会使得梯度越来越小，直至出现“梯度消失”问题。ReLU函数在正半轴的导数始终为1，不存在该问题。
计算量更小，相较于Sigmoid函数的指数计算，ReLU函数只是求最大值的过程。
具有稀疏性，ReLU函数在小于0时值为0，减小过拟合的概率，当然也有可能导致某些神经元输出永远都是0，产生神经元死去的现象。

卷积神经网络

网络结构

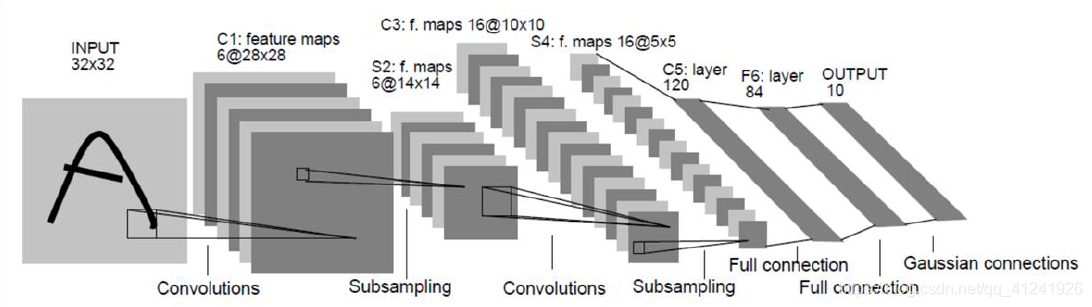
上图是LeNet卷积神经网络的结构(图源自原论文)，它由若干个卷积层、池化层和全连接层组成。上图中，首先对输入的$32\times32$图像进行卷积操作(后面会详细解释)得到6个尺寸为$28\times28$的feature map，然后进行下采样也就是池化操作得到6张$14\times14$的map，之后再进行卷积操作得到16张$10\times10$的map，然后是池化得到16张$5\times5$的map，最后就是我们之前讲过的全连接层将$16\times5\times5$经过几个全连接层分至10类。

我们可以看到卷积神经网络的结构为：

输入图像$\to$若干卷积层$\to$一个池化层$\to$若干卷积层$\to$一个池化层$\to ......\to$全连接层

接下来介绍卷积和池化如何操作。

卷积操作Conv

这里举例说明卷积操作，这里用一个$3\times3$的卷积核(filter) 对$5\times5$的图像进行卷积，这个过程通俗的来讲就是将卷积核游走在被卷积的图像上，对应位置相乘求和得到最后的feature map。

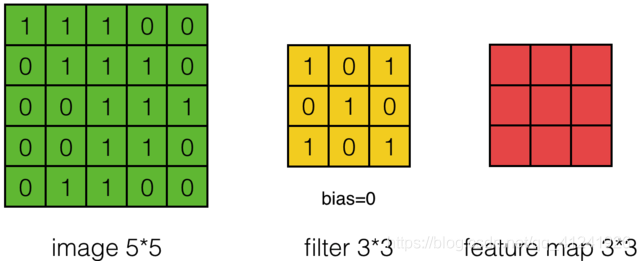
比如对feature中的第一个元素计算过程如下图，卷积核元素和图像元素对应乘积再求和：

\[1\times1+1\times0+1\times1+0\times0+1\times1+1\times0+0\times1+0\times0+1\times1=4 \]

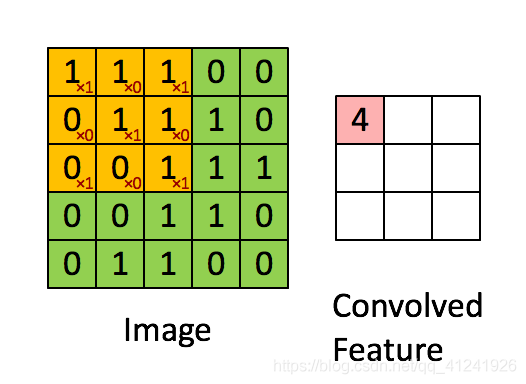
整个卷积过程可用下图表示：

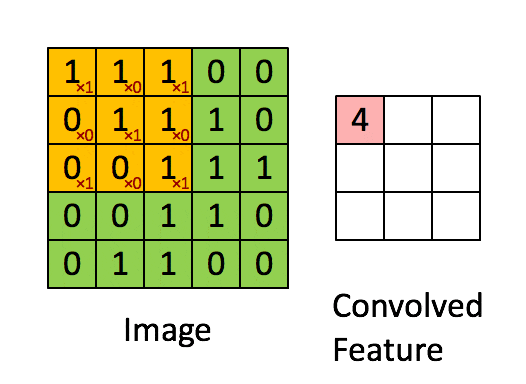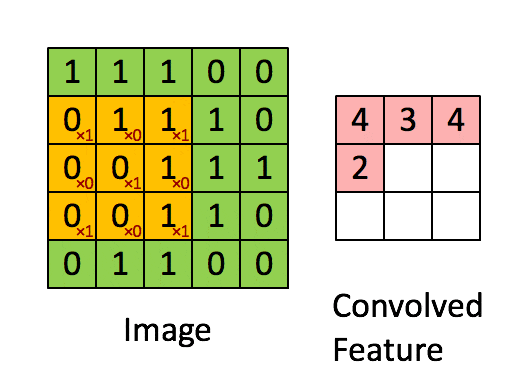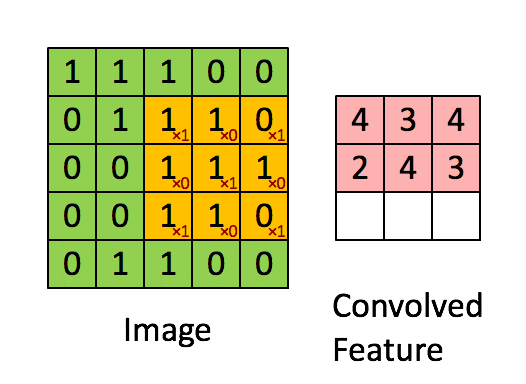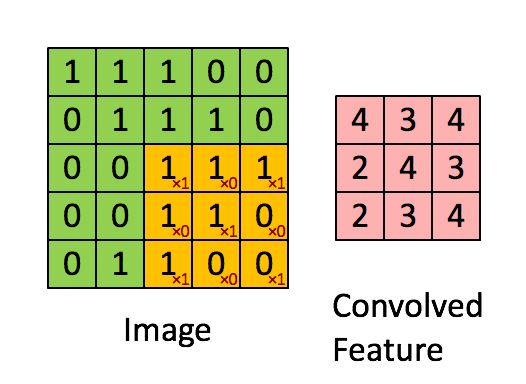
上面演示的就是最简单的卷积操作，卷积有几个重要的参数：

卷积核大小：F，就是filter的宽度。
步幅Stride：S，步幅至卷积核一次游走的像素间隔，上面演示的卷积步幅为1。
补零Zero Padding：Z，Padding就是指在卷积之前对图像四周进行补零的圈数。从上面的卷积过程可以看到，我们从$5\times5$的图像卷积后得到了$3\times3$的图像，有时候我们希望图像不减小，那么可以通过事先在原图像上进行四周补零实现。

这里还有一个十分重要的公式，就是卷积前后图像大小关系，假设卷积前图像宽度$W_1$，卷积后的feature map宽度为$W_2$，它们的关系用下式表示：

\[ W_2 = [(W_1 - F + 2\times Z)/S ]+ 1 \]

上面的中括号为向下取整操作。

对于一开始提到的卷积神经网络中，第一次卷积得到了6张feature map，这其实就是在一张图像中用多个不同的卷积核进行卷积形成的，不同的卷积核对应不同的通道，也就是说我们通过不同的卷积核得到不同的map。

接下来的问题就是如何对多通道的图像进行卷积呢？或者说上面6通道的feature map如何进行卷积呢？其实很简单，我们只要每个通道对应一个卷积核就行了，具体过程用下图表示：

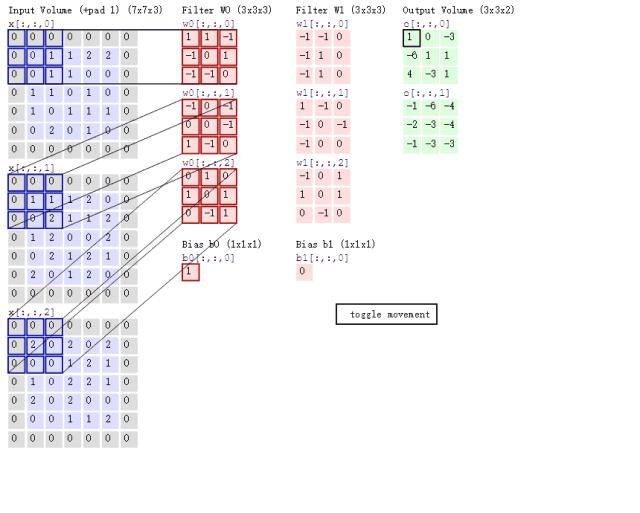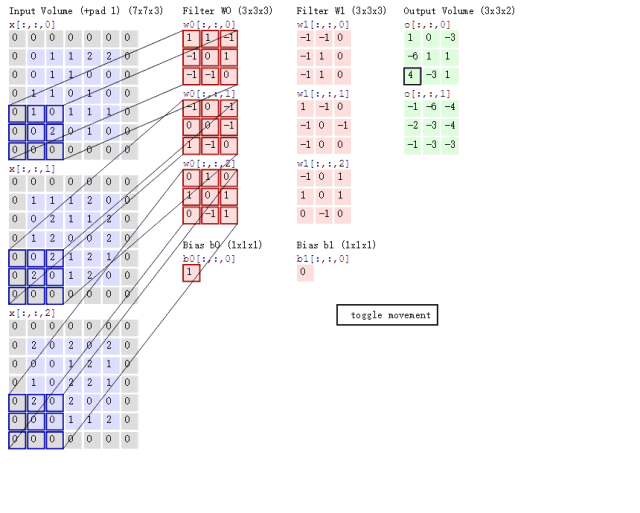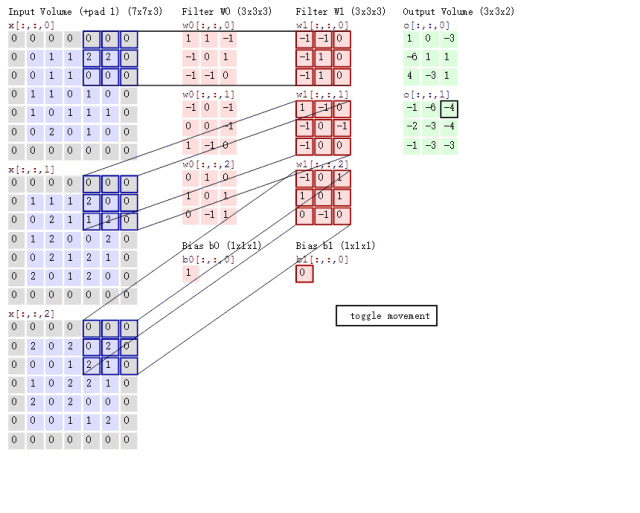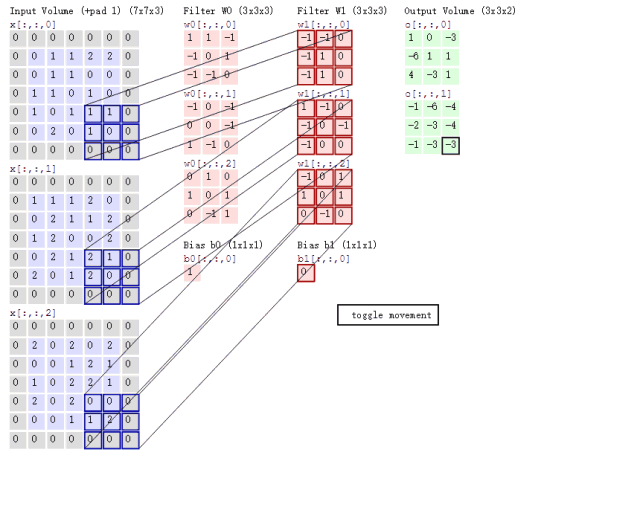
这里对一张3通道的图像进行卷积，那么我们的卷积核必须也是三通道的，也就是$3\times 3\times 3$的卷积核卷积后能得到一张新的map，上图中用了两个$3\times 3\times 3$的核得到了2张map。

池化操作

池化操作一般来说是一个下采样的过程。可以进一步的减小feature map的大小从而减小参数的数量。Pooling的方法有很多，常见的类型有最大值池化(Max Pooling)和均值池化(Average Pooling)，最大值池化的过程见下图：

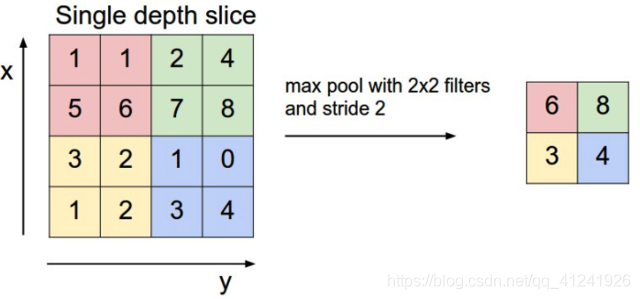
Pooling操作同样有和卷积操作一样的三个参数：filter，stride和padding，Pooling操作前后的图像大小关系也和卷积一致。也就是满足下面关系：

$ W_2 = [(W_1 - F + 2Z)/S ]+ 1 $

其中括号为向下取整。

卷积神经网络LeNet5

LeNet 5是Yann LeCun教授在1998年提出的一种卷积神经网络，被用于手写数字的识别，准确率达到了99.2%，这个网络也具备了当今卷积神经网络的全部要素。网络结构图开篇已经给出：

结构为：

Type	kernel size / stride	output size
Conv	$5\times 5 / 1$	$6\times 28\times 28$
Pooling	$2\times 2 / 1$	$6\times 14\times 14$
Conv	$5\times 5 / 1$	$16\times 10\times 10$
Pooling	$2\times 2 / 1$	$16\times 5\times 5$
FC	-	$120$
FC	-	$84$
FC	-	$10$

可以看到一共是7层结构，网络比较简单，接下来我们通过pytorch编写一个LeNet 5对MNIST手写数字进行分类，看看它的表现到底怎么样。

LeNet5 实现

这里有两点说明：

LeNet 5输入的图像为$32\times 32$，Mnist数据集的图像大小为$28\times28$，可以将图像resize，torchvision.transform就有resize的变换方法；我这里是直接将第二个卷积操作的卷积核改为$3\times3$，这样就能够匹配。（目前的示例都是直接使用torch的数据集，这里推荐大家也可以自己编写Dataset类，torch的官方教程有介绍）
LeNet 5的激活函数采取的仍然是Sigmoid函数，ReLU是Alex在2012年的AlexNet中提出并使用的，这里我直接使用ReLU函数，因为这个激活函数效果更好，也更常用。

这里给出网络搭建的代码：

import torch
import torch.nn as nn
import torch.nn.functional as f
from torch.utils.data import DataLoader
from torchvision import datasets, transforms

# 优先选择gpu
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")


# LeNet 5用于对Mnist数据集分类
class CnnNet(nn.Module):
    def __init__(self):
        super(CnnNet, self).__init__()
        # 5*5卷积核卷积
        self.conv1 = nn.Conv2d(1, 6, (5, 5))
        # 3*3卷积核卷积（为了输入28*28能够匹配，原网络是5*5卷积核）
        self.conv2 = nn.Conv2d(6, 16, 3)  # 卷积核为方阵的时候可以只传入一个参数
        self.pool = nn.MaxPool2d((2, 2))
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        """
        前向传播函数，返回为一个size为[batch_size,features]的向量
        :param x:
        :return:
        """
        # 卷积+relu+池化
        x = self.pool(f.relu(self.conv1(x)))
        x = self.pool(f.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = f.relu(self.fc1(x))
        x = f.relu(self.fc2(x))
        x = self.fc3(x)
        return x


# 训练网络
def train(train_loader):
    # 损失函数值
    running_loss = 0.0
    for i, data in enumerate(train_loader, 0):
        inputs, labels = data
        # 如果有gpu，则使用gpu
        inputs, labels = inputs.to(device), labels.to(device)

        # 梯度置零
        optimizer.zero_grad()
        # 前向传播
        output = net(inputs)
        # 损失函数
        loss = criterion(output, labels)
        # 反向传播，权值更新
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        # 每50个batch_size后打印一次损失函数值
        if i % 100 == 99:
            print('%5d loss: %.3f' %
                  (i + 1, running_loss / 100))
            running_loss = 0.0


# 训练完1个或几个epoch之后，在测试集上测试以下准确率，防止过拟合
def test(test_loader):
    correct = 0
    total = 0
    # 不进行autograd
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)
            outputs = net(images)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()

    print('Accuracy of the network on test images: %d %%' % (
            100 * correct / total))
    return correct / total


if __name__ == '__main__':
    # Pytorch自带Mnist数据集，可以直接下载，分为测试集和训练集
    train_dataset = datasets.MNIST(root='./data/', train=True, transform=transforms.ToTensor(), download=True)
    test_dataset = datasets.MNIST(root='./data/', train=False, transform=transforms.ToTensor(), download=True)
    # DataLoader类可以实现数据集的分批和打乱等
    train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=16, shuffle=False)
    test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=16, shuffle=False)

    net = CnnNet().to(device)
    # 准则函数使用交叉熵函数，可以尝试其他
    criterion = nn.CrossEntropyLoss()
    # 优化方法为带动量的随机梯度下降
    optimizer = torch.optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
    for epoch in range(20):
        print('Start training: epoch {}'.format(epoch+1))
        train(train_loader)
        test(test_loader)

代码比较简单，就不过多说明，代码也有部分注释。网络的结构比较简单，训练起来也比较快，如果电脑有NVIDIA的显卡的话训练更快。在我的电脑上训练完第8轮之后，测试集上的准确率达到了0.98，参数只是粗略的给了一下，可以尝试修改优化的损失函数以及优化方法进行训练。不管怎么说，这已经是一个非常好的成绩了，相比全连接网络而言更优秀。

总结

这篇文章主要介绍了卷积神经网络的一般结构，重点介绍了卷积操作（Conv）和池化操作（Pooling）的具体运算，最后简单介绍了LeNet 5网络并用它对Mnist数据集进行了分类。

Type	kernel size / stride	output size
Conv	\(5\times 5 / 1\)	\(6\times 28\times 28\)
Pooling	\(2\times 2 / 1\)	\(6\times 14\times 14\)
Conv	\(5\times 5 / 1\)	\(16\times 10\times 10\)
Pooling	\(2\times 2 / 1\)	\(16\times 5\times 5\)
FC	-	\(120\)
FC	-	\(84\)
FC	-	\(10\)