对极几何
先放一张图 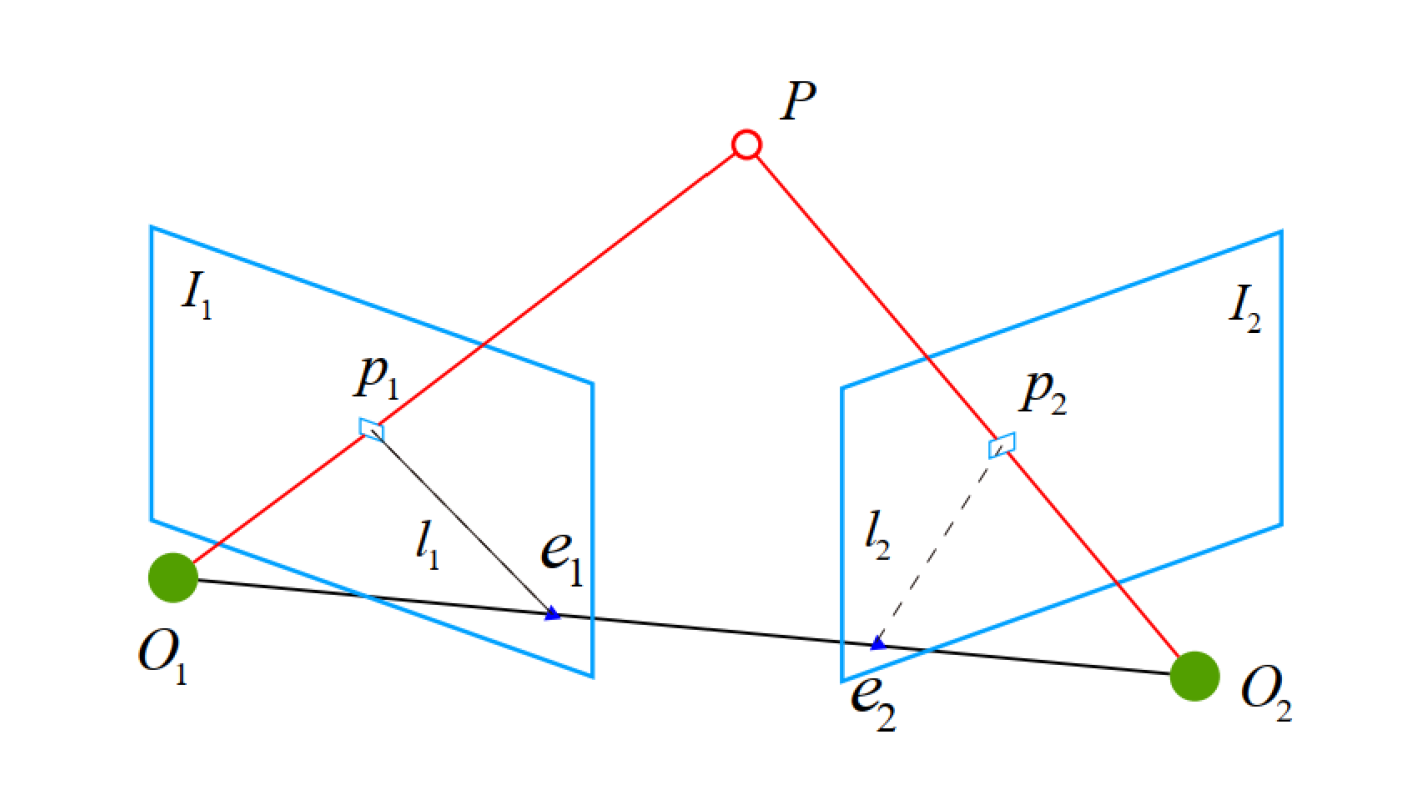
设第一帧到第二帧的运动为\(R,t\),两个相机中心分别为\(O_1,O_2\)。\(p_1\)是\(I_1\)中的特征点,对应到\(I_2\)中的特征点为\(p_2\)。下面通过一些术语来描述他们之间的几何关系。首先,连线\(\vec{O_1 p_1}\)和连线\(\vec{O_2 p_2}\)在三维空间中相交于\(P\),这是\(O_1,O_2,P\)可以确定一个平面,称为极平面,\(O_1,O_2\)连线与像平面\(I_1,I_2\)的交点分别为\(e_1,e_2\),\(e_1,e_2\)被称为极点,\(O_1O_2\)被称为基线,我们称极平面与两个像平面\(I_1,I_2\)之间的相交线\(l_1,l_2\)为极线。
基础矩阵
对于特征点对\(p_1,p_2\),用基础矩阵\(F_{21}\)描述特征点对之间的转换关系
\[ p_2^TF_{21}p_1=0 \]
写成矩阵形式,有
\[ \begin{bmatrix} v_2&u_2&1 \end{bmatrix} \begin{bmatrix} f_1&f_2&f_3\\f_4&f_5&f_6\\f_7&f_8&f_9 \end{bmatrix} \begin{bmatrix} u_1\\v_1\\1 \end{bmatrix}=0 \]
展开得到
\[ \begin{bmatrix} u_1*u_2&v_1*u_2&u_2&u_1*v_2&v_1*v_2&v_2&u_1&v_1&1 \end{bmatrix} \begin{bmatrix} f_1\\f_2\\f_3\\f_4\\f_5\\f_6\\f_7\\f_8\\f_9 \end{bmatrix}=0 \]
这样,每对点提供一个约束方程,基础矩阵共有9个元素,7个自由度,且秩为2,所以8对点提供8个约束方程就可以求解F。
本质矩阵
本质矩阵E和基础矩阵F差了个相机内参矩阵,恢复位姿的时候一般通过本质矩阵恢复,这样可以屏蔽因为相机内参造成的影响。本质矩阵和基础矩阵的关系为
\[ E=K^TFK , E=t^{\land}R \]
从本质矩阵恢复相机位姿\(R,t\)
对E进行奇异值分解(SVD),对于任意一个E,存在两个可能的\(R,t\)与其对应,又因为-E和E等价,所以对任意一个t取负号,得到的结果是一样的,因此通过本质矩阵E分解到\(R,t\)时,一共存在4个可能的解。幸运的是,正确的解是唯一的,只有第一个解的空间点P在两个相机中都具有正的深度。
\[ t_1^{\land}=UR_Z(\frac{\pi}{2})DU^T,R_1=UR^T_Z(\frac{\pi}{2})V^T \] \[ t_2^{\land}=UR_Z(-\frac{\pi}{2})DU^T,R_2=UR^T_Z(-\frac{\pi}{2})V^T \]
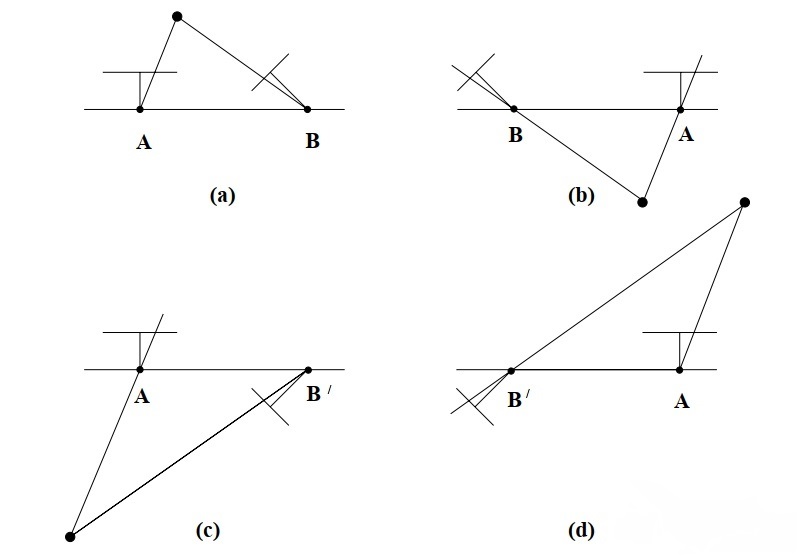
三角测量(三角化)
已知一对匹配好的特征点\(x_1,x_2\),投影矩阵\(P_1,P_2\)分别将同一个空间点X投影到两幅图中的\(x_1,x_2\)。
描述为:
\[ x_1=\lambda P_1X \] \[ x_2=\lambda P_2X \]
对于每一个表达式可以用通用方程来描述: \[ \begin{bmatrix} x\\y\\1 \end{bmatrix}=\lambda \begin{bmatrix} p_1&p_2&p_3&p_4\\p_5&p_6&p_7&p_8\\p_9&p_10&p_11&p_12 \end{bmatrix} \begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} \]
简记为 \[ \begin{bmatrix} x\\y\\1 \end{bmatrix}=\lambda \begin{bmatrix} -&P_0&-\\-&P_1&-\\-&P_2&-\end{bmatrix} \begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} \]
两边叉乘x,有 \[ \begin{bmatrix} 0&-1&y\\1&0&-x\\-y&x&0 \end{bmatrix} \begin{bmatrix} -&P_0&-\\-&P_1&-\\-&P_2&-\end{bmatrix} \begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} = \begin{bmatrix} 0\\0\\0 \end{bmatrix} \]
一个点就有
\[ \begin{bmatrix} yP_2-P_1\\P_0-xP_2\\xP_1-yP_0 \end{bmatrix} X = \begin{bmatrix} 0\\0\\0 \end{bmatrix} \]
秩为2,取前两行就够了
一对点的情况如下:
\[ \begin{bmatrix} y_1P_{12}-P_{11}\\P_{10}-x_1P_{12}\\y_2P_{22}-P_{21}\\P_{20}-x_2P_{22} \end{bmatrix} X = \begin{bmatrix} 0\\0\\0 \end{bmatrix} \]
变成最小二乘问题,用奇异值分解即可求解X
各向同性归一化(八点法)
利用8点法求基础矩阵不稳定的一个主要原因就是原始的图像像点坐标组成的系数矩阵A不好造成的,而造成A不好的原因是像点的齐次坐标各个分量的数量级相差太大。基于这个原因,在应用8点法求基础矩阵之前,先对像点坐标进行归一化处理,即对原始的图像坐标做同向性变换,这样就可以减少噪声的干扰,大大的提高8点法的精度。
预先对图像坐标进行归一化有以下好处:
- 能够提高运算结果的精度
- 利用归一化处理后的图像坐标,对任何尺度缩放和原点的选择是不变的。归一化步骤预先为图像坐标选择了一个标准的坐标系中,消除了坐标变换对结果的影响。
归一化操作分两步进行,首先对每幅图像中的坐标进行平移(每幅图像的平移不同)使图像中匹配的点组成的点集的形心(Centroid)移动到原点;接着对坐标系进行缩放使得点\(p=(x,y,w)^T\)中的各个分量总体上有一样的平均值,各个坐标轴的缩放相同的,最后选择合适的缩放因子使点p到原点的平均距离是\(\sqrt{2}\)。 概括起来变换过程如下:
- 对点进行平移使其形心位于原点。
- 对点进行缩放,使它们到原点的平均距离为\(\sqrt{2}\)
- 对两幅图像独立进行上述变换
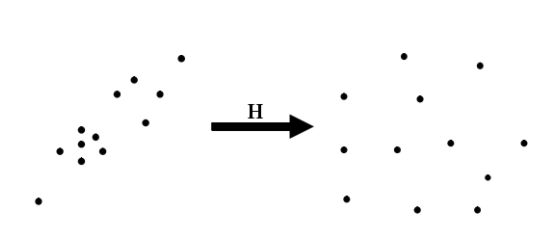
上图左边是原始图像的坐标,右边是归一化后的坐标,H是归一化的变换矩阵,可记为如下形式:
\[ T=S \begin{bmatrix} 1&0&-\bar{u}\\0&1&-\bar{v}\\0&0&\frac{1}{S} \end{bmatrix} \] 其中,\(\bar{u},\bar{v}\)是图像点坐标两个分量的平均值
\[ \bar{u}=\frac{1}{N}\sum_{i=1}^N u_i,\bar{v}=\frac{1}{N}\sum_{i=1}^N v_i \]
S表示尺度,其表达式为:
\[ S=\frac{\sqrt{2}\cdot N}{\sqrt{\sum_{i=1}^N (u_i-\bar{u})^2+(v_i-\bar{v})^2}} \]
注:这里的公式很多网上的博客都错了,分子的N应该在根号外面,这样平均距离才是\(\sqrt{2}\),OpenCV的八点法归一化函数也是这样做的
这样,首先对原始的图像坐标进行归一化处理,再利用8点法求解基础矩阵,最后将求得的结果解除归一化,得到基础矩阵F,总结如下:
- 对图像1进行归一化处理,计算一个只包含平移和缩放的变换\(T_1\),将图像1中的匹配点集\(p_i^1\)变换到新的点集\(\hat{p_i^1}\),新点集的形心位于原点\((0,0)^T\),并且它们到原点的平均距离是\(\sqrt{2}\)。
- 对图像2,计算变换矩阵\(T_2\)进行相同的归一化处理
- 使用8点法利用变换后的点集估计基础矩阵\(\hat{F}\)
- 建立变换\(F=T^T_2\hat{F} T_1\)
对单应矩阵的归一化处理同理,总结如下:
- 对图像1进行归一化处理,计算一个只包含平移和缩放的变换\(T_1\),将图像1中的匹配点集\(p_i^1\)变换到新的点集\(\hat{p_i^1}\),新点集的形心位于原点\((0,0)^T\),并且它们到原点的平均距离是\(\sqrt{2}\)。
- 对图像2,计算变换矩阵\(T_2\)进行相同的归一化处理
- 使用8点法利用变换后的点集估计基础矩阵\(\hat{H}\)
- 建立变换\(H=T^{-1}_2 \hat{H}T_1\)
ORB-SLAM2中的归一化操作与论文中的不同,是采取了一阶矩进行归一化,具体来说就是缩放因子分别为
\[ sX=\frac{N}{\sum_{i=1}^N \begin{vmatrix}u_i-\bar{u} \end{vmatrix}}, sY=\frac{N}{\sum_{i=1}^N \begin{vmatrix}v_i-\bar{v} \end{vmatrix}} \]
至于为什么这样做,还没搞明白。


