奇异值分解SVD
SVD分解定义
\[ A=U\sum{}V^T \]
其中,A是\(m\times n\)的矩阵,根据奇异值分解后,U是\(m\times m\)的矩阵,\(\sum{}\)是一个\(m\times n\)的矩阵,除主对角线上的元素以外全部为0,主对角线上的每个元素都称为奇异值,V是一个\(n\times n\)的矩阵,U和V都是酉矩阵,即满足
\[ U^TU=I,V^TV=I \]
可以用下图表示奇异值分解:
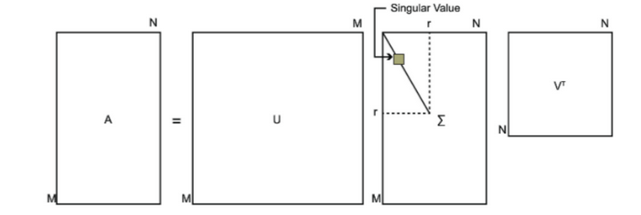
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。 也就是说,我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说:
\[ A_{m\times n}=U_{m\times n}\sum{}_{m\times n}V^T_{n\times n}\approx U_{m\times k}\sum{}_{k\times k}V^T_{k\times n} \]
其中k比n小很多,也就是一个大矩阵A可以用三个小矩阵\(U_{m\times k},\sum{}_{k\times k},V^T_{k\times n}\)来表示。
SVD求解最小二乘问题:
\[ min\begin{Vmatrix} Ax-b \end{Vmatrix}^2,A\in R^{m\times n},x\in R^{n},b\in R^{m} \]
m个方程求n个未知数,有三种情况:
- \(m=n\)且A非奇异,则有唯一解(线性代数学到的)
- \(m>n\),约束的个数超过未知数个数,称为超定问题
- \(m<n\),约束的个数小于未知数个数,称为负定/欠定问题
通常我们遇到的都是超定问题,此时是没有解的,从而转向最小二乘问题:
\[ J(x)=min\begin{Vmatrix} Ax-b \end{Vmatrix}^2 \]
懒得敲公式了。上个链接 奇异值分解与最小二乘法
总结一下结论,对于\(Ax=0\)
SVD分解之后得到的V最右侧的列向量(也就是\(V^T最下方的行向量\))就是一般性齐次线性方程组\(Ax=0\)的解。


